我国农村居民人均消费支出回归模型
一、研究目的
2003年中国农村人口占59.47％，而消费总量却只占41.4%，农村居民的收入和消费是一个值得研究的问题。消费模型是研究居民消费行为的常用工具。通过中国农村居民消费模型的分析可判断农村居民的边际消费倾向，这是宏观经济分析的重要参数。同时，农村居民消费模型也能用于农村居民消费水平的预测。
二、模型设定
正如第二章所讲述的，影响居民消费的因素很多，但由于受各种条件的限制，通常只引入居民收入一个变量做解释变量，即消费模型设定为
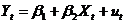
式中，Yt为农村居民人均消费支出，Xt为农村人均居民纯收入，ut为随机误差项。表5-1是从《中国统计年鉴》收集的中国农村居民1985-2003年的收入与消费数据。
表5-1 1985-2003年农村居民人均收入和消费 单位：元
| 年份 |
全年人均纯收入 （现价） |
全年人均消费性支出 （现价） |
消费价格指数 （1985=100） |
人均实际纯收入 （1985可比价） |
人均实际消费性支出 （1985可比价） |
| 1985 1986 1987 1988 1989 1990 1991 1992 1993 1994 1995 1996 1997 1998 1999 2000 2001 2002 2003 |
397.60 423.80 462.60 544.90 601.50 686.30 708.60 784.00 921.60 1221.00 1577.70 1923.10 2090.10 2162.00 2214.30 2253.40 2366.40 2475.60 2622.24 |
317.42 357.00 398.30 476.70 535.40 584.63 619.80 659.80 769.70 1016.81 1310.36 1572.10 1617.15 1590.33 1577.42 1670.00 1741.00 1834.00 1943.30 |
100.0 106.1 112.7 132.4 157.9 165.1 168.9 176.8 201.0 248.0 291.4 314.4 322.3 319.1 314.3 314.0 316.5 315.2 320.2 |
397.60 399.43 410.47 411.56 380.94 415.69 419.54 443.44 458.51 492.34 541.42 611.67 648.50 677.53 704.52 717.64 747.68 785.41 818.86 |
317.40 336.48 353.42 360.05 339.08 354.11 366.96 373.19 382.94 410.00 449.69 500.03 501.77 498.28 501.75 531.85 550.08 581.85 606.81 |
注：资料来源于《中国统计年鉴》1986-2004。
为了消除价格变动因素对农村居民收入和消费支出的影响，不宜直接采用现价人均纯收入和现价人均消费支出的数据，而需要用经消费价格指数进行调整后的1985年可比价格计的人均纯收入和人均消费支出的数据作回归分析。
根据表5-1中调整后的1985年可比价格计的人均纯收入和人均消费支出的数据，使用普通最小二乘法估计消费模型得
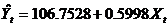模型一
Se= (12.2238) (0.0214)
t= (8.7332) (28.3067)
R2 =0.9788，F = 786.0548，d f = 17，DW = 0.7706
该回归方程可决系数较高，回归系数均显著。对样本量为19、一个解释变量的模型、5%显著水平，查DW统计表可知，dL=1.18，dU= 1.40，模型中DW<dL，显然消费模型中有自相关。这一点残差图中也可从看出，点击EViews方程输出窗口的按钮Resids可得到残差图，如图5-1所示。
图5-1 残差图
图5-1残差图中，残差的变动有系统模式，连续为正和连续为负，表明残差项存在一阶正自相关，模型中t统计量和F统计量的结论不可信，需采取补救措施。
三、自相关问题的处理
为解决自相关问题，选用科克伦—奥克特迭代法。由模型可得残差序列et，在EViews中，每次回归的残差存放在resid序列中，为了对残差进行回归分析，需生成命名为e的残差序列。在主菜单选择Quick/Generate Series或点击工作文件窗口工具栏中的Procs/ Generate Series，在弹出的对话框中输入e = resid，点击OK得到残差序列et。使用et进行滞后一期的自回归，在EViews命今栏中输入ls e e (-1)可得回归方程
et=0.4960 et-1
由上式可知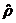
=0.4960，对原模型进行广义差分，得到广义差分方程
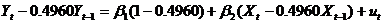
对上式的广义差分方程进行回归，在EViews命令栏中输入ls Y-0.4960*Y (-1) c X-0.4960*X(-1)，回车后可得方程输出结果如表5-2。
| 表5-2广义差分方程输出结果 |
| Dependent Variable: Y-0.496014*Y(-1) |
| Method: Least Squares |
| Date: 03/26/05 Time: 12:32 |
| Sample(adjusted): 1986 2003 |
| Included observations: 18 after adjusting endpoints |
| Variable |
Coefficient |
Std. Error |
t-Statistic |
Prob. |
| C |
60.44431 |
8.964957 |
6.742287 |
0.0000 |
| X-0.496014*X(-1) |
0.583287 |
0.029410 |
19.83325 |
0.0000 |
| R-squared |
0.960914 |
Mean dependent var |
231.9218 |
| Adjusted R-squared |
0.958472 |
S.D. dependent var |
49.34525 |
| S.E. of regression |
10.05584 |
Akaike info criterion |
7.558623 |
| Sum squared resid |
1617.919 |
Schwarz criterion |
7.657554 |
| Log likelihood |
-66.02761 |
F-statistic |
393.3577 |
| Durbin-Watson stat |
1.397928 |
Prob(F-statistic) |
0.000000 |
由表5-2可得回归方程为
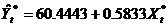模型二
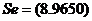（0.0294）
t = （6.7423）（19.8333）
R2= 0.9609 F= 393.3577 d f = 16 DW = 1.3979
式中，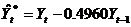
，
。
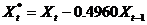由于使用了广义差分数据，样本容量减少了1个，为18个。查5%显著水平的DW统计表可知dL = 1.16，dU = 1.39，模型中DW = 1.3979>dU，说明广义差分模型中已无自相关，不必再进行迭代。同时可见，可决系数R2、t、F统计量也均达到理想水平。
对比模型一、模型二，很明显普通最小二乘法低估了回归系数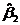
的标准误差。[原模型中Se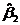（）= 0.0214，广义差分模型中为Se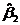（）= 0.0294。
经广义差分后样本容量会减少1个，为了保证样本数不减少，可以使用普莱斯—温斯腾变换补充第一个观测值，方法是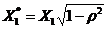
和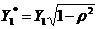
。在本例中即为
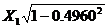和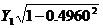
。由于要补充因差分而损失的第一个观测值，所以在EViews中就不能采用前述方法直接在命令栏输入Y和X的广义差分函数表达式，而是要生成X和Y的差分序列X*和Y*。在主菜单选择Quick/GenerateSeries或点击工作文件窗口工具栏中的Procs/Generate Series，在弹出的对话框中输入Y*=Y-0.4960*Y (-1)，点击OK得到广义差分序列Y*，同样的方法得到广义差分序列X*。此时的X*和Y*都缺少第一个观测值，需计算后补充进去，计算得
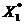=345.236，
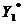=275.598，双击工作文件窗口的X* 打开序列显示窗口，点击Edit+/-按钮，将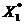=345.236补充到1985年对应的栏目中，得到X*的19个观测值的序列。同样的方法可得到Y*的19个观测值序列。在命令栏中输入Ls Y* c X*得到普莱斯—温斯腾变换的广义差分模型为
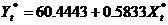模型三
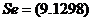（0.0297）
t = （6.5178）（19.8079）
R2 = 0.9585 F = 392.3519 d f = 19 DW = 1.3459
对比模型二、模型三可以发现，两者的参数估计值和各检验统计量的差别很微小，说明在本例中使用普莱斯—温斯腾变换与直接使用科克伦—奥克特两步法的估计结果无显著差异，这是因为本例中的样本还不算太小。如果实际应用中样本较小，则两者的差异会较大。通常对于小样本，应采用普莱斯—温斯腾变换补充第一个观测值。
由差分方程有
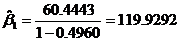
由此，我们得到最终的中国农村居民消费模型为
Y t=119.9292+0.5833 X t
由上式的中国农村居民消费模型可知，中国农村居民的边际消费倾向为0.5833，即中国农民每增加收入1元，将增加消费支出0.5833元。