案例分析3
一、研究目的和模型设定
依据凯恩斯宏观经济调控原理,建立简化的中国宏观经济调控模型。经理论分析,采用基于三部门的凯恩斯总需求决定模型,在不考虑进出口的条件下,通过消费者、企业、政府的经济活动,分析总收入的变动对消费和投资的影响。设理论模型如下:
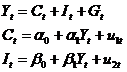
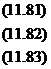
其中,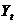 为支出法GDP,
为支出法GDP,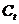 为消费,
为消费,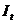 为投资,
为投资,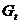 为政府支出;内生变量为
为政府支出;内生变量为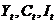 ;前定变量为
;前定变量为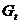 ,即M=3,K=1。
,即M=3,K=1。
二、模型的识别性
根据上述理论方程,其结构型的标准形式为
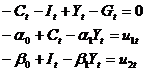
标准形式的系数矩阵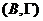 为
为
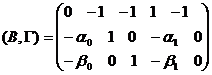
由于第一个方程为恒定式,所以不需要对其识别性进行判断。下面判断消费函数和投资函数的识别性。
1、消费函数的识别性
首先,用阶条件判断。这时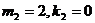 ,因为
,因为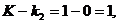 并且
并且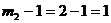 ,所以
,所以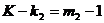 ,表明消费函数有可能为恰好识别。
,表明消费函数有可能为恰好识别。
其次,用秩条件判断。在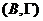 中划去消费函数所在的第二行和非零系数所在的第一、二、四列,得
中划去消费函数所在的第二行和非零系数所在的第一、二、四列,得
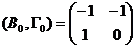
显然,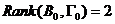 ,则由秩条件,表明消费函数是可识别。再根据阶条件,消费函数是恰好识别。
,则由秩条件,表明消费函数是可识别。再根据阶条件,消费函数是恰好识别。
2、投资函数的识别性
由于投资函数与消费函数的结构相近,判断过程与消费函数完全一样,故投资函数的阶条件和秩条件的判断予以省略。结论是投资函数也为恰好识别。
综合上述各方程的判断结果,得出该模型为恰好识别。
三、宏观经济模型的估计
由于消费函数和投资函数均为恰好识别,因此,可用间接最小二乘估计法(ILS)估计参数。选取GDP、消费、投资,并用财政支出作为政府支出的替代变量。这些变量取自1978年——2003年中国宏观经济的历史数据,见表11.1。
表11.1
| 年份 |
支出法GDP |
消费 |
投资 |
政府支出 |
| 1978 |
3605.6 |
2239.1 |
1377.9 |
480.0 |
| 1979 |
4074.0 |
2619.4 |
1474.2 |
614.0 |
| 1980 |
4551.3 |
2976.1 |
1590.0 |
659.0 |
| 1981 |
4901.4 |
3309.1 |
1581.0 |
705.0 |
| 1982 |
5489.2 |
3637.9 |
1760.2 |
770.0 |
| 1983 |
6076.3 |
4020.5 |
2005.0 |
838.0 |
| 1984 |
7164.4 |
4694.5 |
2468.6 |
1020.0 |
| 1985 |
8792.1 |
5773.0 |
3386.0 |
1184.0 |
| 1986 |
10132.8 |
6542.0 |
3846.0 |
1367.0 |
| 1987 |
11784.7 |
7451.2 |
4322.0 |
1490.0 |
| 1988 |
14704.0 |
9360.1 |
5495.0 |
1727.0 |
| 1989 |
16466.0 |
10556.5 |
6095.0 |
2033.0 |
| 1990 |
18319.5 |
11365.2 |
6444.0 |
2252.0 |
| 1991 |
21280.4 |
13145.9 |
7517.0 |
2830.0 |
| 1992 |
25863.7 |
15952.1 |
9636.0 |
3492.3 |
| 1993 |
34500.7 |
20182.1 |
14998.0 |
4499.7 |
| 1994 |
46690.7 |
26796.0 |
19260.6 |
5986.2 |
| 1995 |
58510.5 |
33635.0 |
23877.0 |
6690.5 |
| 1996 |
68330.4 |
40003.9 |
26867.2 |
7851.6 |
| 1997 |
74894.2 |
43579.4 |
28457.6 |
8724.8 |
| 1998 |
79003.3 |
46405.9 |
29545.9 |
9484.8 |
| 1999 |
82673.1 |
49722.7 |
30701.6 |
10388.3 |
| 2000 |
89340.9 |
54600.9 |
32499.8 |
11705.3 |
| 2001 |
98592.9 |
58927.4 |
37460.8 |
13029.3 |
| 2002 |
107897.6 |
62798.5 |
42304.9 |
13916.9 |
| 2003 |
121511.4 |
67442.5 |
51382.7 |
14764.0 |
资料来源:《中国统计年鉴2004》,中国统计出版社。
1、恰好识别模型的ILS估计。
根据ILS法,首先将结构型模型转变为简化型模型,则宏观经济模型的简化型为
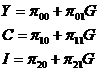
其中结构型模型的系数与简化型模型系数的关系为
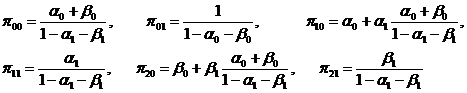
其次,用OLS法估计简化型模型的参数。进入EViews软件,确定时间范围;编辑输入数据;选择估计方程菜单。则估计简化型样本回归函数的过程是:按路径:Qucik/EstimateEguation/ Equation Spesfication,进入”Equation Spesfication”对话框。
在”Equation Spesfication”对话框里,分别键入:”GDP C GOV”、“COM C GOV”、“INVC GOV”,其中,GDP表示Y,COM表示C,INV表示I,GOV表示G。得到三个简化型方程的估计结果,写出简化型模型的估计式:
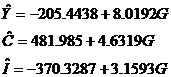
即简化型系数的估计值分别为
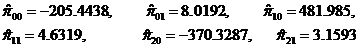
最后,因为模型是恰好识别,则由结构型模型系数与简化型模型系数之间的关系,可惟一地解出结构型模型系数的估计。解得的结构型模型的参数估计值为
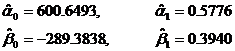
从而结构型模型的估计式为
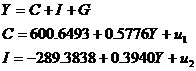
2、过度识别模型的2SLS估计。
考虑在宏观经济活动中,当期消费行为还要受到上一期消费的影响,当期的投资行为也要受到上一期投资的影响,因此,在上述宏观经济模型里再引入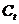 和
和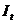 的滞后一期变量
的滞后一期变量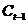 和
和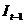 。这时宏观经济模型可写为
。这时宏观经济模型可写为
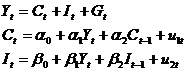
用阶条件和秩条件对上述模型进行识别判断(具体的判断过程从略),结论是消费函数和投资函数均是过度识别。需要运用二段最小二乘法对方程组的参数进行估计。
首先,估计消费函数。进入EViews软件,确定时间范围;编辑输入数据。然后按路径:Qucik/Estimate equation/Equationspecification/Method/TSLS,进入估计方程对话框,将method按钮点开,这时会出现估计方法选择的下拉菜单,从中选“TSLS”,即两阶段最小二乘法。
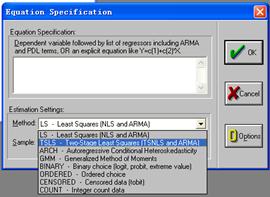
图11.2
当TSLS法选定后,便会出现“EquationSpecification”对话框,见图11.3。
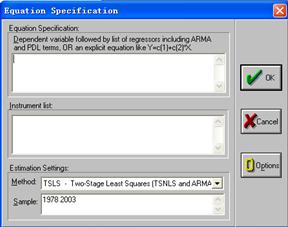
图11.3
“Equation Specification”对话框有两个窗口,第一个窗口是用于写要估计的方程;第二个窗口是用于写该方程组中所有的前定变量,EViews要求将截距项也看成前定变量。具体书写格式如下:第一个窗口写:“COM C GDP COM(-1))”;第二个窗口写:“C GOV COM(-1) INV(-1)”。其中,COM(-1),INV(-1)分别表示消费变量COM和投资变量INV的滞后一期。然后按“OK”,便显示出估计结果,见表11.5。
表11.5
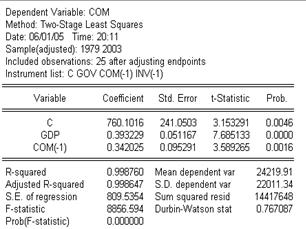
根据表11.5写出消费函数的2SLS估计式为
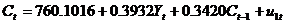
其次,估计投资函数。与估计消费函数过程一样,得到如下估计结果,见表11.6。
表11.6
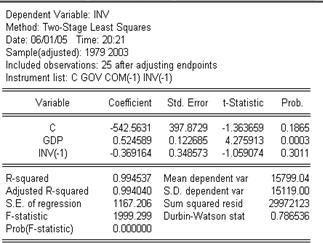
由表11.6写出投资函数的估计式
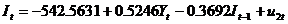
最后,写出该方程组模型的估计式为